Thuật toán tìm kiếm nhị phân Binary Search C++. Cách cài đặt thuật toán, ưu nhược điểm, độ phức tạp. So sánh tìm kiếm nhị phân với tìm kiếm tuần tự. Cùng mình tìm hiểu tất cả trong bài viết này nhé.
1. Thuật toán tìm kiếm
Trong lập trình bạn sẽ thường xuyên gặp phải bài toán tìm kiếm. Tìm kiếm hiểu theo đúng nghĩa đen của nó là chúng ta đi tìm một thứ gì đó. Tất cả các hình thức tìm kiếm như tra google, tìm trên website, ứng dụng, tra cứu tên . . . đều sử dụng thuật toán tìm kiếm.
Trong lập trình tìm kiếm dùng để tìm vị trí, truy vấn phần tử cần tìm trong dữ liệu xử lý từ đó thực hiện các thao tác cần thiết. Vì nó được sử dụng rất nhiều nên đây là một trong số các thuật toán cực kì quan trọng với mỗi lập trình viên.
Bạn sẽ dễ dàng nghe thấy 5 dạng thuật toán tìm kiếm phổ biến nhất đó là:
- Tìm kiếm tuyến tính – Sequential search hay còn gọi là Linear search
- Tìm kiếm nhị phân – Binary search
- Thuật toán Ternary Search
- Thuật toán Jump Search
- Thuật toán Exponential Search
Hai thuật toán mình liệt kê đầu thường được nhắc đến nhiều nhiều hơn. Trong đó thuật toán tìm kiếm tuyến tính là thuật toán đơn giản nhất và được sử dụng nhiều nhất vì nó đơn giản và thực sự dễ hình dung. Tuy nhiên tốc độ, sự tối ưu của nó thuộc vào loại thấp nhất, đây là lý do bạn nên trang bị thêm một số thuật toán tìm kiếm khác.
Bài toán tìm kiếm trong bài viết này mình nêu ra như sau: Cho mảng arr[] đã sắp xếp có n phần tử, viết hàm tìm kiếm trả về chỉ số của phần tử có giá trị x trong arr[]. (tìm vị trí của x trong mảng)
Xem thêm các thuật toán quan trọng trong lập trình tại đây.
2. Thuật toán tìm kiếm nhị phân – Binary search
Thuật toán tìm kiếm nhị phân (Binary search) hay còn gọi là thuật toán tìm kiếm chia đôi, tìm kiếm nửa khoảng, binary chop là thuật toán có ứng dụng tính chất chia để trị. Ta sẽ tiến hành chia đôi mảng ban đầu, nếu phần tử ở giữa lớn hơn, hoặc nhỏ hơn phần tử cần tìm ta sẽ thu hẹp miền cần tìm về hai đầu tương ứng. Tiếp tục làm như vậy cho tới khi hết mảng hoặc tìm ra vị trí phần tử cần tìm.
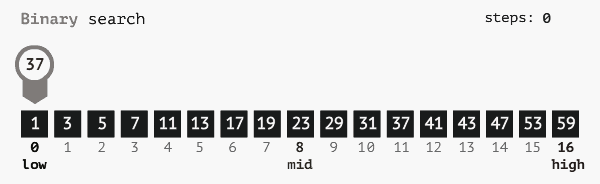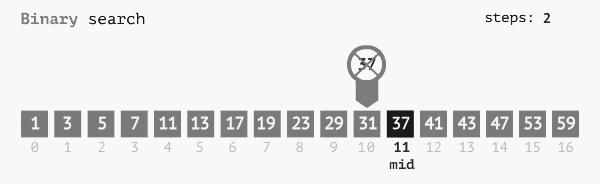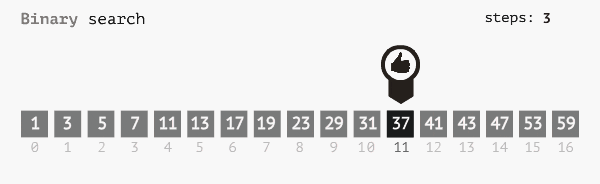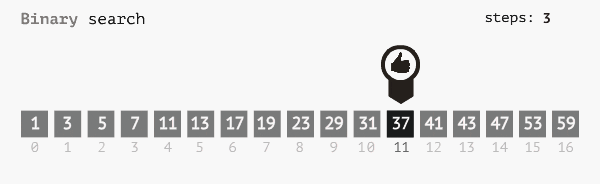
Ý tưởng thuật toán tìm kiếm nhị phân:
- Chia mảng ban đầu thành 2 phần, lấy mid làm phần tử giữa: mid = (left + high) /2;
- Nếu arr[mid] == x thì trả về vị trí của mid
- Nếu x < arr[mid] lúc này x chắc chắn sẽ ở bên trái. Đệ quy thuật toán tìm x ở mảng bên trái.
- Nếu x > arr[mid] lúc này x sẻ ở bên phải mid. Đệ quy thuật toán tìm xở mảng bên phải
- Nếu không có phần tử thỏa mãn ta trả về -1
Cài đặt thuật toán bằng C/C++:
int binary_Search(int arr[], int low, int high, int x) {
if (high >= low) { // Trong khi chưa xét hết
int mid = low + (high - low) / 2; // Tương đương mid = (low + high)/2;
if (arr[mid] == x) // Nếu phần tử mid bằng phần tử tìm kiếm thì dừng
return mid;
if (arr[mid] > x) // Nếu x nhỏ hơn mid, đệ quy tìm bên trái
return binary_Search(arr, low, mid - 1, x);
return binary_Search(arr, mid + 1, high, x); // Nếu x > mid ta đệ quy tìm kiếm nửa bên phải
}
return -1; // Nếu không tìm thấy ta trả về -1;
}
Đánh giá thuật toán tìm kiếm nhị phân:
Độ phức tạp trung bình: O (logn)
Độ phức tạp tốt nhất: O(1)
Độ phức tạp không gian: O(1)
3. So sánh tìm kiếm nhị phân với tìm kiếm tuyến tính
Khác với tìm kiếm tuyến tính – Linear sort sẽ sử dụng vòng lặp duyệt từ đầu mảng lần lượt về phía cuối mảng cho tới khi tìm được phần tử cần tìm thì sẽ dừng lại. Để dễ hiểu, bạn xem hình minh họa so sánh Binary search với Sequential phía dưới.
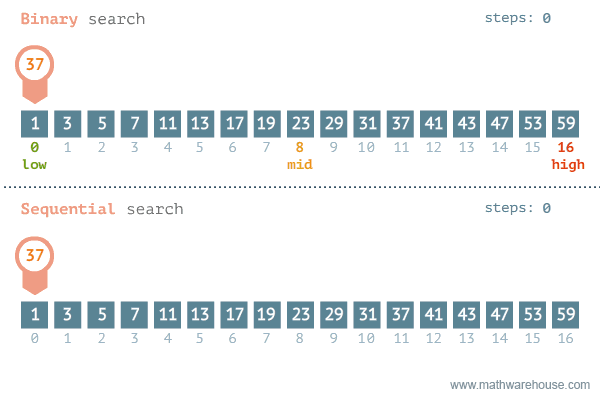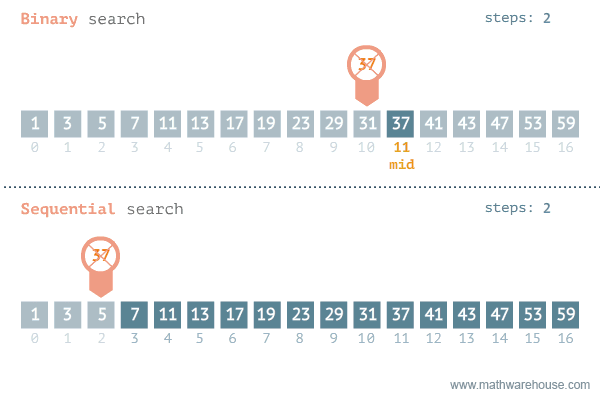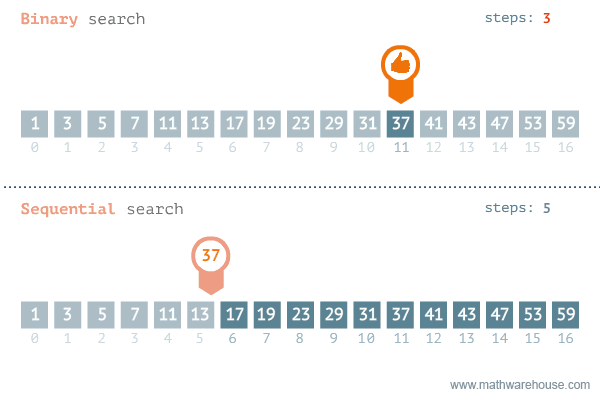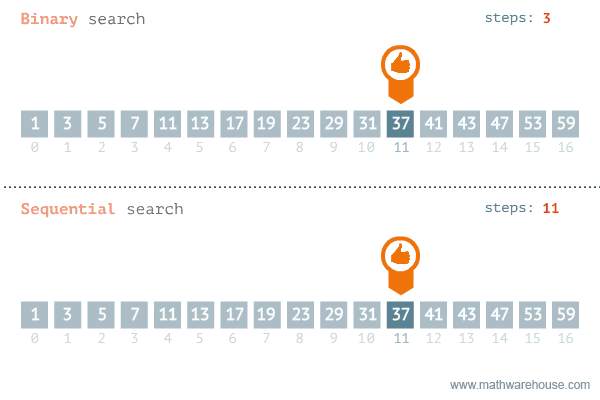
Một số ưu nhược điểm giữa hai thuật toán với nhau:
- Tìm kiếm nhị phân chỉ hoạt động trên mảng đã sắp xếp có thứ tự
- Tìm kiếm nhị phân phù hợp với mảng có độ dài lớn
- Thuật toán tìm kiếm nhị phân có hiệu xuất tốt hơn
- Tìm kiếm tuần tự phù hợp với mảng nhỏ và chưa sắp xếp.
- . . .
Ngoài ra còn có nhiều ưu nhược điểm khác nữa
Lời kết: Cảm ơn bạn đã đọc đến những dòng cuối cùng trên bài viết của mình. Nếu có thắc mắc gì đừng ngại để lại comment xuống phía dưới bài viết nhé!
Chúc bạn thành công!
