Bài toán biến đổi xâu A thành xâu B code C/C++

Bài toán biến đồi xâu C/C++, tìm số bước nhỏ nhất biến đổi xâu a về xâu b. Một bài toán xử lý xâu cực hay và có chút nâng cao ứng dụng thuật toán quy hoạch động để giải quyết.

1. Giới thiệu bài toán

Biến đổi xâu là một trong số bài toán điển hình minh họa dễ hiểu nhất cho việc sử dụng thuật toán quy hoạch động. Bài toán này có chút tương đồng với bài tìm xâu con chung lớn nhất.

Đề bài:
Viết chương trình biến đổi xâu x=(x₁,x₂,…, x_n) và y=(y₁,y₂, …, y_m) tìm số thao tác nhỏ nhất để biến đổi xâu x về xâu y.
Ví dụ: xâu ‘cat’ và ‘cut’ cần 1 phép toán biến đổi kí tự ‘a’ thành ‘u’.

Như vậy bài toán có 1 vấn đề chính cần tập trung: Tìm số bước biến đổi để xâu a thành xâu b.
Ngoài ra có thể mở rộng thêm bằng việc đưa ra các phép biến đổi đó.

Mình đánh giá bài toán không khó để hiểu và giải quyết. Mấu chốt ở việc bạn hiểu được công thức xử lý của nó. Và điểu đặc biệt, bạn cần nắm rõ kiến thức về xâu và mảng đa chiều trong C/C++ nhé!

2. Ý tưởng giải quyết bài toán

Ý tưởng giải quyết trong bài viết này mình có tham khảo từ diễn đàn olympic tin học VNOI.INFO. Dựa vào đó, mình cũng làm luôn phần truy vết để tìm ra các bước biến đổi cụ thể.

Mình gọi tắt hai xâu ở đây là A và B nhé, nếu bạn thích có thể chỉnh thành X và Y.
n là chiều dài xâu A.
m là chiều dài xâu B.

Trước tiên về các phép biến đổi, tại vị trí i, j có 3 cách:

1. Xóa một kí tự A[i] ở xâu a
2. Thay kí tự A[i] thành kí tự B[j]
3. Chèn kí tự B[j] sau A[i]

Số bước biến đổi tại vị trí i của xâu A sẽ phụ thuộc vào vị trí j của xâu B nên ta sẽ dùng mảng hai chiều để lưu kết quả.

Gọi L[i][j] là số bước biến đổi nhỏ nhất để i ký tự đầu tiên của xâu A thành j kí tự đầu của xâu B.
Ta có:

• L[0][j] = j và L[i][0] = i
• L[n][m] sẽ là số bước nhỏ nhất để biến A thành B

Tại một vị trí L[i][j] bất kì ta có những trường hợp sau:

• A[i] == B[j] , đây là trường hợp hai kí tự tại vị trí đang xét bằng nhau ta có: L[i][j] = L[i-1][j-1]
• Ngược lại chọn gia L[i][j] nhỏ nhất trong 3 trường hợp biến đổi:
  • Xóa kí tự A[i]
    • Xâu A thành : A[1]A[2]. . .A[i-1]
    • Xâu B: B[1]B[2] . . . B[j-1]B[j]
    • L[i][j] = L[i-1][j] + 1 (do có 1 phép biến đổi nên + 1)
  • Thay A[i] thành B[j]:
    • Xâu A : A[1][2]. . . A[i-1]B[j]
    • Xâu B: B[1]B[2] . . . B[j-1]B[j]
    • L[i][j] = L[i-1][j-1] + 1
  • Chèn B[j] vào sau A[i]
    • Xâu A : A[1][2]. . . A[i-1]A[i]B[j] // Phần này nhìn bảng kết quả là hiểu. i lúc nào cũng chạy sau j
    • Xâu B: B[1]B[2] . . . B[j-1]B[j]
    • Khi đó xâu A[i] thành xâu B[j-1] ta có: L[i][j] = L[i][j-1] + 1

Tóm lược lại công thức như sau:

• Nếu A[i] == B[j] thì: L[i][j] = L[i-1][j-1]
• Ngược lại (A[i] != B[j] ) thì: L[i][j] = min (L[i-1][j], L[i-1][j-1], L[i][j-1]) + 1;

Phần truy vết các bước bạn sẽ duyệt từ vị trí L[n][mư, xác định 3 trường hợp tương tự như lúc xây dựng bảng kết quả.

Để dễ hiểu hơn, bạn xem hình minh họa của mình dưới đây nhé!

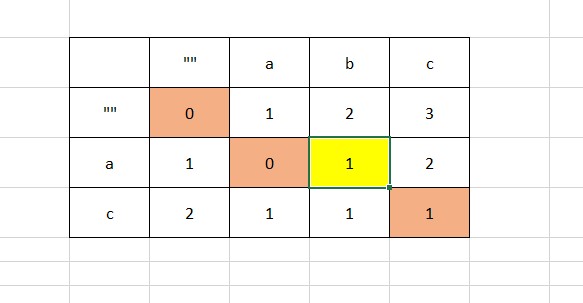
Dễ thấy trong hình ảnh trên, các ô sẽ đi theo đường nhỏ nhất. Kết quả ở đây là 1 phép biến đổi : chèn b

3. Code C/C++ bài toán biến đổi xâu

Cùng tham khảo code của mình nhé!

/*By https://duongdinh24.com*/
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;

// Hàm tìm min
int min(int a, int b, int c){
	if(a<=b && a<=c)
		return a;
	else if(b < a && b<=c)
		return b;
	else
		return c;
}

// Hàm đếm số bước chuyển đổi xâu
void changeString(string a, string b){
	int step;  // Biến lưu số bước
	int n = a.size();  // Độ dài xâu a
	int m = b.size();  // Độ dài xâu b
	int L[n+1][m+1];   // Mảng kết quả 
// thêm 1 bởi vì có 1 hàng và 1 cột cho L[0][j], L[i][0]
	
	// j =0, L[i][0] = i;
	for(int i=0; i<=n; i++)
		L[i][0] = i;
	// i = 0; L[0][j] = j;
	for(int j=0; j<=m; j++){
		L[0][j] = j;
	}
	
// Duyệt mảng kết quả: hàng trước, cột sau. Hàng xâu A, cột xâu B
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m; j++){
			if(a[i-1] == b[j-1]) // nếu bằng nhau
				L[i][j] = L[i-1][j-1];
			else{ // nếu khác nhau
			     // min của 3 trường hợp
				L[i][j] = min(L[i-1][j], L[i-1][j-1], L[i][j-1] ) + 1;
			}
		}
	}	
	
	step = L[n][m];  // gán kết quả
	cout<<"\nSo buoc: "<<step<<"\n";  // in ra màn hình
// Truy vết
	int i = n;
	int j = m;
	while(i >=0 && j >=0){  // Nếu còn chưa qua vị trí cuối cùng
		if(a[i-1] == b[j-1]){  // Bằng nhau tức k có phép biến đổi
			i--;
			j--;
		}
		else{
			// Trường hợp xóa kí tự
			if( L[i-1][j] <= L[i-1][j-1] &&  L[i-1][j] <= L[i][j-1]){
				cout<<"Xoa "<<a[i-1]<<"\n";
				i--;
			}
			// Trường hợp sửa kí tự
			else if( L[i-1][j-1] < L[i-1][j] && L[i-1][j-1] <= L[i][j-1]){
				cout<<"Thay "<<a[i-1]<<" => "<<b[j-1]<<"\n";
				i--;
				j--;
			}
			// Trường hợp chèn kí tự
			else{
				cout<<"Chen "<<b[j-1]<<" sau "<<a[i-1]<<"\n";
				j--;
			}
			
		}
	}
}

int main(){
	string a, b;
        // Nhập hai xâu từ bàn phím
	cout<<"Nhap xau a: "; cin>>a;
	cout<<"Nhap xau b: "; cin>>b;
        // Gọi hàm xử lý 
	changeString(a,b);
	return 0;
}

Trên đây là toàn bộ cách giải và chương trình cài đặt cho bài toán này. Bạn có thể dựa vào đó để tự sáng tạo ra cách giải cho riêng mình nhé!

Xem thêm bài viết khác về ứng dụng thuật toán tại đây.
Cảm ơn bạn đã ghé thăm blog của mình <3.